服务区确定后停放车设施最佳区位分析模型

从一批候选位置(或区域)中选取一定的位置,建设公共设施(点),为本区域中其它区域 (需求点)提供服务的区位模型(Location allocation model),国内外学者已经作了大量研究,主要有P中心问題(PWP)模型等。如果假设设施点可以分配到平面内任意一个位置,需求点与设施点距离为欧氏直线距离,则称为平面选址模型。在服务区确定后单个停放车设施最佳区位分析时,可以先忽略掉实际走行路线的扭曲,假设停放车设施与服务范围内各服务对象可以直线联结,此时,停放车最佳位置由下列模型确定: 

min∑f(x_i)r_i

s.t.   r_i ∈  D

式中f(x_i)——服务范围内第i个服务对象点的停放车需求量。

r_i——停车点与第i个服务对象点的直线距离,其位置应该位于服务范围空间D内。ri也可写成:

r_i = [(x₀ - x_i))2 + (y₀ - y_i)²]^1/2

式中:x₀、y₀——停放车设施中心点的位标,为第i个服务对象点的坐标。

对目标函数求导,可以得到:

x₀=∑[f(x_i)x_i/r_i] / ∑[f(x_i)/r_i]

y₀=∑[f(x_i)y_i/r_i] / ∑[f(x_i)/r_i]

对公式的求解,--般可用迭代法,即首先以重心坐标  x'₀=∑f(x_i)x_i / ∑f(x_i)、y'₀=∑f(x_i)y_i / ∑f(x_i)作为

初始值代人,经过若干次迭代循环后就可以得到最优解,其程序可归结为

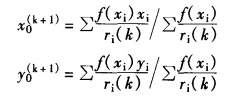
对比上述模型,可发现与韦伯的工业区位运输费用最低点选址计算模型一致,这一方面验证了本模型计算结果可以使停车者的总出行成本(时间)最低,另一方面也说明了停车区位与别的区位,如市场与道路区位的冲突。以十字交叉道路四象限有建筑为例,极端情况下(四象 限停车需求相等、距十字中心点距离相等)最佳停车中心点位置为交叉口中心。因此,本模塱 计算结果只是停放车选址最佳位置的理想状态点,实际工作中需结合具体情况(如建筑布局、 交通道路布设、其它竞争性用地效用对比后)才能确定出备选停放车位置。

1.模型一般形式构造及分析

机动车停车场服务半径一般局限在300 ~ 500m以内,如果较这样的距离还远,则使用者出于方便性考虑,往往会弃车而改乘公交车辆。在300~500m距离内,停车场使用者一般面对的道路形态如图所示。

为了表述清楚,在图的抽象图形中分别引入坐标系,并假设备选停车服务范围内各点处的停车密度函数为f(x,y)如图所示,在图情况下,可以以出行距离最短为目标,列出最佳停车场选址点的目标方程。

设停车场的位置坐标为x₀ 、y₀ ,出行者要达到的最终地点坐标为x₁ 、y₁ 。,则一般由于沿原有道路走可以减少行走中的障碍,停车者的路径选择一般多为停车场~附近道路~目的地。

为了减少非道路行走的不确定性,以及可能遇到的障碍,道路不通或其他麻烦,任一停车者在选择路径时往往走的是这三者之间的最短路,如图所示。

也即停车后行走距离分别为丨y₀|、丨x₁-x₀丨、y₁。停车场的设置,应当使停车后行走的时 间最短,今设停车场~附近道路~目的地的速度分别为v₁,v₂,v₃,则最佳停车场选址位置必须应满足:

由于坐标系的建立是任意的,而且理想的停车位置应紧靠公路边,d₁的距离往往很小,故我们可用停车场边缘道路处位置作为坐标原点,忽略停车后步行距离,并进行座标轴平移变形 后,即x₀= 0,y₀ = 0,此时,上述目标函数可化为:

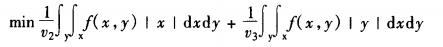
可看出为使目标函数最小,则当f(x_i,y_i)越大时,应使|x_i|、|y_i|越小。即:要最大限度的降低上述目标函数,必需要使停车场位置与停车使用密度大的地区尽可能接近,但同时要兼顾其它区使用者状况。特别地,当停车服务区内密度函数为恒定数时,且v₁=v₂=v₃时,停车场位于服务的中心时即为最佳位置;当密度函数不同,但v₁=v₂=v₃时,停车场的最佳位置 以停车服务区接近重心点处为较佳。一般地,由于v2往往大于v₁,v₃,故既比较靠近道路边 缘,又接近停车使用较密集的地点为停车场的较佳选择点。这一结果,如果用地受限时,可以适当移动。

2.模型实际应用的求解方法

在实际应用中,可以计算每个服务对象与停放车设施备选点的费用函数值(如时间或广义费用),然后将不同选址方案所有服务过程产生的总时间或广义费用汇总,即可以得到不同选 址状况时成本或费用总额情况,取成本或费用总额最小的方案就可以确保使用者步行最为方 便的实现。对于路权函数的计算,首先可以借用最短路交通量分配或容量限制最短路交通量分配算法,得到停车服务区各路段上车辆行驶、行人的路径选择结果,然后调用流量——成本模型即可以实现分路段、分方式费用函数的汇总,最后将所有路段加总,就可以得到不同备选方案的费用额度。如果备选点不固定,而是在一定可行域内选择,此时,可以一定的步长,通过路径选择优化算法的结合而使模型应用范围扩展为网络型选址模型。组合以上分析,其推荐算法法流程为:

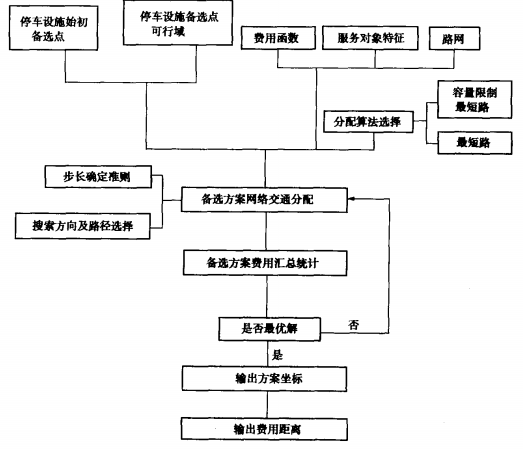
流程图中,主要有三个分析子模块:交通分配模块、费用汇总与比较模块、停车设施备选点步长与搜索方向确定模块。前两个模块的研究比较成熟,对第三个模块,需一开始多入几个搜索备选点,通过好的迭代算法等,将可能域扩展至整个影响区并使搜索效率得以提高。

上海祁舜道闸专业服务：上海道闸车牌识别系统，车牌自动‌‌‌‌识别系统，无人值守停车管理系统，智慧停车场管理，智能人行通道，道闸，智能道闸，智能车位引导系统，停车场无感支付系统，门禁安装 ，人行通道翼闸、三辊闸、速通闸等，上海地区可上面测量，免费设计安装。

网站：http://www.qishunzn.com/

• 官网：www.qishunzn.com

• 热线：15900830396（微信同号）  

• 电话：021-56161178

• 地址：上海市宝山区美丹路222号640室（美兰湖地铁站）

• 邮箱：qishunjianzhu@126.com

• 业务部：罗先生  15902126928

• 业务部：刘女士  15221009051

• 业务QQ：2207171446